A Review of Binary Search Trees

My previous computer science review post took a look at the tree data structure. This time around we will be exploring a specific kind of binary tree: The Binary Search Tree.

Let’s not waste any more time and just jump right in!

What is a Binary Search Tree?

A Binary Search Tree (BST) is a binary tree such that the following holds true:

• The left sub-tree contains only nodes whose values are less than the parent’s value.
• The right sub-tree contains only nodes whose values are greater than the parent’s value.
• The left and right sub-trees must themselves be a valid binary search tree.

Here’s an example of a valid binary search tree:

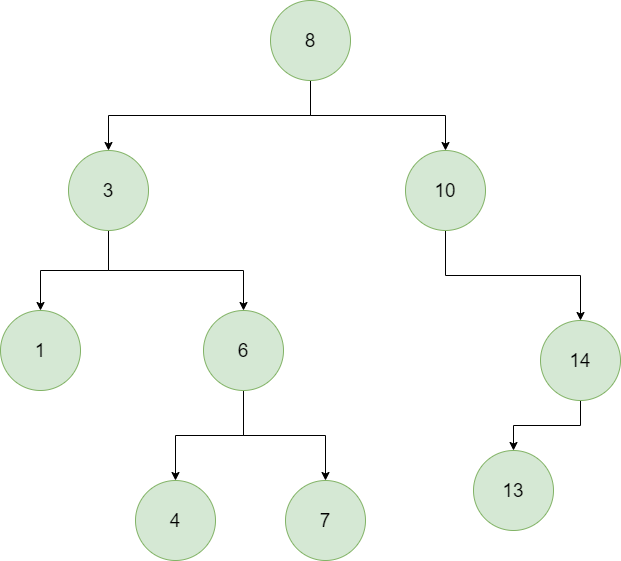
The ordering that these properties enforce is what gives the binary search tree its power. By having all of the values (or keys) ordered, operations like searching and finding the max/min value can be done relatively quickly. In fact, the time complexity for operations on a BST turns out to be O(h), where h is the height of the tree.

If the tree was unordered, however, the worst case would be having to search every node in the tree, which means that we effectively have no benefit over just using an unordered list!

Searching a BST

Searching a binary search tree is very similar to performing a binary search on a sorted list. We start at the root node and compare it’s value with our target. If it’s equal, we’re done. If the target is less than the current node’s value, we move to the left sub-tree, else we move to the right sub-tree. We repeat this process until we’ve either found our target or searched the entire tree.

Let’s look at what this search might look like in Java:

 1// Searches for a node in a binary search tree
 2public Node search(Node root, int key) {
 3    if (root == null || root.data == key) // base case
 4        return root;
 5    if (root.data < key)
 6        // Key is greater than current node, search the right sub-tree
 7        return search(root.right, key);
 8    // Key is smaller than root's key, search the left sub-tree
 9    return search(root.left, key);
10}

From this, it shouldn’t be too much of a stretch to see that the best case for a binary search tree is when the BST is a balanced tree. When this occurs, searching goes from being O(h) to being O(log n). This is why self-balancing trees can be beneficial, but we’ll cover those in future posts.

Insertion into a BST

When searching for a location to insert a new node into a binary search tree, we traverse the tree from the root down to the leaves of the tree. Along the way, we make comparisons to decide if we should continue traversing the left or right sub-tree (remember, smaller values to the right and larger values to the left). In this way, a new node will always be inserted as a leaf in the tree.

Consider inserting the value 16 into the following BST:

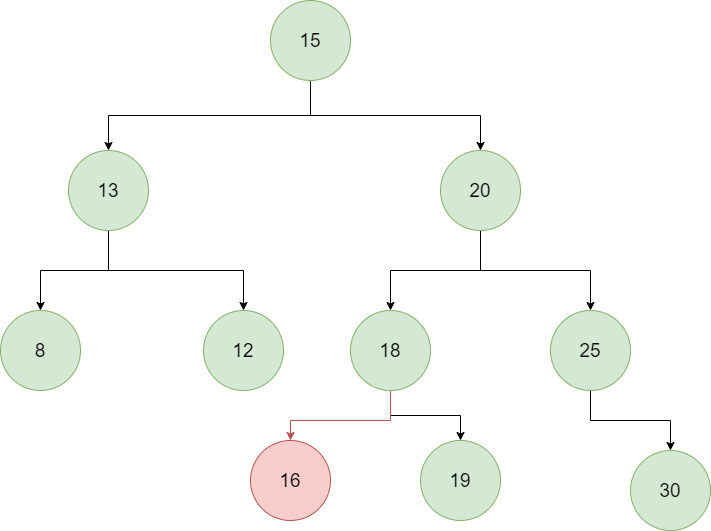
Let’s take a look at what this insertion code might look like in Java:

 1public Node insert(Node root, int key) {
 2    // Base case, perform the insertion
 3    if (root == null) {
 4        root = new Node(key);
 5        return root;
 6    }
 7    // Recurse the tree to find insertion point
 8    if (key < root.data)
 9        root.left = insert(root.left, key);
10    else if (key > root.data)
11        root.right = insert(root.right, key);
12    return root;
13}

Deleting from a BST

There are three possible scenarios when trying to remove a value from a binary search tree:

1) The node to be deleted is a leaf

This is the simplest scenario. Here we only need to delete the node.

2) The node to be deleted has only one child

In this case, we copy the child to the parent and then delete the child node.

3) The node to be deleted has two children

In this case, we need to determine the inorder successor of the node and copy its contents to the parent node and delete the inorder successor.

Let’s take a look at how we could implement this in our Java example:

 1// Locates a minimum value in a BST
 2public int findMinimumValue(Node root) {
 3    int min = root.data;
 4    while (root.left != null) {
 5        min = root.left.data;
 6        root = root.left;
 7    }
 8    return min;
 9}
10// Deletes a value from a BST
11public Node delete(Node root, int key) {
12    // Base case
13    if (root == null)
14        return root;
15    // recurse down the tree
16    if (key < root.data)
17        root.left = delete(root.left, key);
18    else if (key > root.data)
19        root.right = delete(root.right, key);
20    else {
21        // The key is the same as root's, this is the node to be deleted
22        if (root.left == null)
23            return root.right;
24        else if (root.right == null)
25            return root.left;
26        root.data = findMinimumValue(root.right);
27        root.right = delete(root.right, root.data);
28    }
29    return root;
30}